A statistical method frequently used in clinical research in recent years: Causal mediation analysis

Son yıllarda klinik araştırmalarda sıkça kullanılan bir istatistiksel metod: Nedensel aracılık analizi

Meral Yay

¹Department of Statistics, Mimar Sinan Fine Arts University, Faculty of Arts and Sciences, Istanbul, Türkiye

DOI : 10.5606/tgkdc.dergisi.2023.98553

In recent years, in addition to treatment and outcome variables, mediator variables have been also included in the statistical models used in clinical studies. These mediating variables are usually used as confounding factors in studies and are attempted to be controlled using multivariate regression models according to the type of outcome variable. However, the confounding factors in the models are insufficient to reveal the variable that plays a mediating role between treatment and outcome variables. If researchers have prior knowledge that another explanatory variable has a direct or indirect effect on the outcome, they may want to reflect this in the model and reveal the causal effect indirectly. In this case, there is a mediator variable that indirectly transfers the causal effect. With the help of causal mediation analysis in observational and randomized-controlled trials, it becomes possible to generate evidence about situations in which interventions and exposures may affect health outcomes. The first study on causal mediation analysis, which emerged with this need, was on the concept of "mediated or indirect effects in pathway models of the inheritance of skin color in guinea pigs" introduced by Sewall Wright in 1920. Subsequently, Hyman in 1955 and Lazarsfeld in 1955 provided the original definitions of how a third variable influences the relationship between two variables through a series of statistical tests that were later translated into decomposition of effects by Alwin and Hauser in 1975, mediation in psychology by James and Brett in 1984 and Baron and Kenny in 1986, and evaluation by Judd and Kenny in 1981. The extremely rapid innovations in mediation analysis in recent years, particularly in the last three or four decades, have played an important role in the development of the analysis and a better understanding of its basis.

Mediation analysis is based on statistical modelling. A simple linear regression model would be the right way to convey basic information about the construct. Statistical modelling uses regression analysis to estimate the relationships between the explanatory variable "X" (or treatment variable; independent variable) and outcome (dependent) variable "Y". In its simplest form, the model can be visualized as in Figure 1 by expressing it as in Equation 1:

Figure 1. Simple regression model.

(1) Y=i₁+cX+e₁

In this model, the effect of X on Y is measured by "c" and is called the total effect model, as it does not take into account any other variables. The coefficient "e1" shows the part of Y that is not explained by its relation to the variable X. To transform this simple linear regression model into a mediation model, it is sufficient to add a mediator variable to the model. In other words, in its simplest form, the model for mediation analysis is to insert an M mediator between X and Y.[1] This study aims to explain the continuous outcome model-based mediation analysis based on linear equations. There is only one mediator variable in the model and it is called the "simple mediation model". The equations of the model are as given in Equation 2. and Equation 3. and the model can be visualized as in Figure 2.

Figure 2. Simple mediation model.

(2) Y=i₂+c' X+bM+e₂

(3) M=i₃+aX+e₃

In the causal mediation model, which reveals the relationship between the explanatory and outcome variables with the help of a variable called "mediator", the existence of a third variable is investigated in the relationship between two variables. In the model, X is explanatory, M mediator and Y are outcome variables. c' is the coefficient for the effect of X on Y adjusting for M (direct effect), b is the effect of M on Y adjusting for explanatory variable, a is the coefficient relating to the effect of X on M. e2, e3 are residuals[2] that are uncorrelated with the variables in the right side of the equation and are independent to each other. The causal mediation effect is represented by the product coefficient of ab. Consequently, the total effect c can be expressed as the sum of the direct effect c' and the indirect effect ab and is given by c=c'+ab. The indirect effect due to the presence of the mediating variable is equal to the difference between the parameters c and c'. In the model, the parameters for the direct c' and indirect ab effects of X on Y are different from the total effect. That is, it is unnecessary to test the null hypothesis c=0, as even if the total causal effect is zero, the causal mediation effect may not be zero,[3,4] reflecting the cancellation of effects coming from different pathways.

Mediation analysis is used to identify the mediating variables that transmit the effect of the independent variable on the outcome and to measure the magnitude and test the significance of the indirect effect.[5] Since the publication of Baron and Kenny's seminal article,[6] mediation analysis has been used in thousands of studies in health, social and behavioral sciences. For instance, it has been the method of choice to determine the mechanisms through which an intervention to reduce human immunodeficiency virus (HIV)/ sexually transmitted disease (STD) risk increases the likelihood of condom use,[7] how healthcare worker resilience affects well-being,[8] and how physical health affects mental health.[9] With the help of all these studies, the assumptions and procedure for identifying causal direct and indirect effects can be accurately defined. Among the most important assumptions of mediation analysis is that it assumes that the residuals in Equation 2 and Equation 3 for the indirect effect are independent and that the mediating variable and the residuals in Equation 2 are independent. In addition to these assumptions, the distribution of the indirect effect is assumed to follow a normal distribution. In addition to the Baron and Kenny steps, it is necessary to check whether the indirect effect of the independent variable on the outcome variable is significant to mention the presence of any mediating variable in the mediation model. Among the many tests developed for this purpose, the most frequently used one is the "Sobel test", also known as the "delta method".[10] In the model with a single mediator variable, ab values, which are expressed as mediating or indirect effects, are obtained by the ordinary least squares method, which is most frequently used in regression analysis. [11] Part of the effect of the explanatory variable on the outcome variable can now be explained by the mediating variable. At this point, it becomes necessary to check the significance of the mediating variable. To test for significance, the product of the obtained prediction values is divided by the standard error of this value and the value obtained from the ratio is compared to the critical value using the standard normal distribution. The standard error needed to test the significance of the mediating effect was introduced by Sobel (1982) and is given by

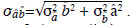
The least squares estimated value of the mediating effect is divided by its standard deviation to transform the variable "z" and it is calculated with 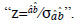The value obtained is compared with the critical value of the standard normal curve areas. When the "z" value calculated is greater than the standard normal distribution critical value, it is decided that the mediation effect does not occur by chance, that is, it is significant. In other words, the null hypothesis "Ho: there is no mediating effect" is rejected and the mediation effect is statistically significant. It is also possible to test the significance of the mediating effect with the confidence interval obtained for the bootstrap distribution. Different types of confidence intervals can be obtained based on the bootstrap method. These can be listed as bias-corrected, percentile, bias-corrected-accelerated, etc. different types of confidence intervals. Percentile bootstrap confidence intervals are preferred when the variable of interest contains outliers and the estimation is less affected by these outliers; i.e., robust,[12] and when the sample size is smaller than "50".[13] When the sample size is large, the biascorrected bootstrap method is used as an alternative to the percentile bootstrap interval. Since the bootstrap method corrects for bias in the sample distribution, it provides a more reliable interval.[14] The confidence interval obtained according to the bootstrap percentile method is based on two percentile cut-off points for the sample distribution (e.g., 2.5% and 97.5% for ?=0.05). If the confidence interval for the mediating effect using percentile values contains the value "0", the hypothesis "Ho: there is no mediating effect" is accepted. In other words, the effect of the mediating variable is not statistically significant. Obtaining bootstrap confidence intervals for the mediating variable or testing the significance of the mediating effect is quite easy with the help of software programs developed today. The analysis can be easily applied with the help of the "Process" macro plug-in developed by Andrew F. Hayes into the open access "R Project" or "SPSS" program. In this article, only one mediating variable is mentioned and information about the significance of the mediating effect is given. Currently, there are many different types of mediation models with more than one mediating variable, where the mediating variables are located in parallel or sequentially with respect to each other, with the number of mediation models exceeding "100". All of these models can be analyzed with the help of the programs mentioned above. To give examples of recent studies using these models, Suissa et al.[15] examined the role of adiposity as a mediator in the relationship between dietary glycemic load and lipid profiles. In another study, Konig et al.[16] evaluated the extent to which the effect of dulaglutide on cardiovascular risk factors could statistically explain its effects on major cardiovascular events with the help of mediation analysis. We believe that this article, which includes basic information about mediation analysis, provide a guidance for researchers who are willing to conduct studies on this subject.