Mediation analysis is based on statistical modelling. A simple linear regression model would be the right way to convey basic information about the construct. Statistical modelling uses regression analysis to estimate the relationships between the explanatory variable "X" (or treatment variable; independent variable) and outcome (dependent) variable "Y". In its simplest form, the model can be visualized as in Figure 1 by expressing it as in Equation 1:
Figure 1. Simple regression model.
(1) Y=i1+cX+e1
In this model, the effect of X on Y is measured by "c" and is called the total effect model, as it does not take into account any other variables. The coefficient "e1" shows the part of Y that is not explained by its relation to the variable X. To transform this simple linear regression model into a mediation model, it is sufficient to add a mediator variable to the model. In other words, in its simplest form, the model for mediation analysis is to insert an M mediator between X and Y.[1] This study aims to explain the continuous outcome model-based mediation analysis based on linear equations. There is only one mediator variable in the model and it is called the "simple mediation model". The equations of the model are as given in Equation 2. and Equation 3. and the model can be visualized as in Figure 2.
Figure 2. Simple mediation model.
(2) Y=i2+c' X+bM+e2
(3) M=i3+aX+e3
In the causal mediation model, which reveals the relationship between the explanatory and outcome variables with the help of a variable called "mediator", the existence of a third variable is investigated in the relationship between two variables. In the model, X is explanatory, M mediator and Y are outcome variables. c' is the coefficient for the effect of X on Y adjusting for M (direct effect), b is the effect of M on Y adjusting for explanatory variable, a is the coefficient relating to the effect of X on M. e2, e3 are residuals[2] that are uncorrelated with the variables in the right side of the equation and are independent to each other. The causal mediation effect is represented by the product coefficient of ab. Consequently, the total effect c can be expressed as the sum of the direct effect c' and the indirect effect ab and is given by c=c'+ab. The indirect effect due to the presence of the mediating variable is equal to the difference between the parameters c and c'. In the model, the parameters for the direct c' and indirect ab effects of X on Y are different from the total effect. That is, it is unnecessary to test the null hypothesis c=0, as even if the total causal effect is zero, the causal mediation effect may not be zero,[3,4] reflecting the cancellation of effects coming from different pathways.
Mediation analysis is used to identify the mediating
variables that transmit the effect of the independent
variable on the outcome and to measure the magnitude
and test the significance of the indirect effect.[5] Since
the publication of Baron and Kenny's seminal article,[6]
mediation analysis has been used in thousands of
studies in health, social and behavioral sciences. For
instance, it has been the method of choice to determine the mechanisms through which an intervention to
reduce human immunodeficiency virus (HIV)/
sexually transmitted disease (STD) risk increases the
likelihood of condom use,[7] how healthcare worker
resilience affects well-being,[8] and how physical health
affects mental health.[9] With the help of all these
studies, the assumptions and procedure for identifying
causal direct and indirect effects can be accurately
defined. Among the most important assumptions of
mediation analysis is that it assumes that the residuals
in Equation 2 and Equation 3 for the indirect effect are
independent and that the mediating variable and the
residuals in Equation 2 are independent. In addition
to these assumptions, the distribution of the indirect
effect is assumed to follow a normal distribution. In
addition to the Baron and Kenny steps, it is necessary
to check whether the indirect effect of the independent
variable on the outcome variable is significant to
mention the presence of any mediating variable in the
mediation model. Among the many tests developed
for this purpose, the most frequently used one is the
"Sobel test", also known as the "delta method".[10] In
the model with a single mediator variable, ab values,
which are expressed as mediating or indirect effects,
are obtained by the ordinary least squares method,
which is most frequently used in regression analysis.
[11] Part of the effect of the explanatory variable on
the outcome variable can now be explained by the
mediating variable. At this point, it becomes necessary
to check the significance of the mediating variable.
To test for significance, the product of the obtained
prediction values is divided by the standard error
of this value and the value obtained from the ratio
is compared to the critical value using the standard
normal distribution. The standard error needed to test
the significance of the mediating effect was introduced
by Sobel (1982) and is given by
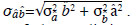
The least squares estimated value of the mediating
effect is divided by its standard deviation to transform
the variable "z" and it is calculated with 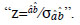 The value obtained is compared with the critical
value of the standard normal curve areas. When the
"z" value calculated is greater than the standard
normal distribution critical value, it is decided that
the mediation effect does not occur by chance, that
is, it is significant. In other words, the null hypothesis
"Ho: there is no mediating effect" is rejected and the
mediation effect is statistically significant. It is also
possible to test the significance of the mediating effect
with the confidence interval obtained for the bootstrap
distribution. Different types of confidence intervals can
be obtained based on the bootstrap method. These can
be listed as bias-corrected, percentile, bias-corrected-accelerated, etc. different types of confidence intervals.
Percentile bootstrap confidence intervals are preferred
when the variable of interest contains outliers and
the estimation is less affected by these outliers; i.e.,
robust,[12] and when the sample size is smaller than
"50".[13] When the sample size is large, the biascorrected
bootstrap method is used as an alternative to
the percentile bootstrap interval. Since the bootstrap
method corrects for bias in the sample distribution, it
provides a more reliable interval.[14] The confidence
interval obtained according to the bootstrap percentile
method is based on two percentile cut-off points for the
sample distribution (e.g., 2.5% and 97.5% for ?=0.05).
If the confidence interval for the mediating effect using
percentile values contains the value "0", the hypothesis
"Ho: there is no mediating effect" is accepted. In
other words, the effect of the mediating variable
is not statistically significant. Obtaining bootstrap
confidence intervals for the mediating variable or
testing the significance of the mediating effect is quite
easy with the help of software programs developed
today. The analysis can be easily applied with the help
of the "Process" macro plug-in developed by Andrew
F. Hayes into the open access "R Project" or "SPSS"
program. In this article, only one mediating variable is
mentioned and information about the significance of
the mediating effect is given. Currently, there are many
different types of mediation models with more than
one mediating variable, where the mediating variables
are located in parallel or sequentially with respect
to each other, with the number of mediation models
exceeding "100". All of these models can be analyzed
with the help of the programs mentioned above. To give
examples of recent studies using these models, Suissa
et al.[15] examined the role of adiposity as a mediator
in the relationship between dietary glycemic load and
lipid profiles. In another study, Konig et al.[16] evaluated
the extent to which the effect of dulaglutide on
cardiovascular risk factors could statistically explain
its effects on major cardiovascular events with the
help of mediation analysis. We believe that this article,
which includes basic information about mediation
analysis, provide a guidance for researchers who are
willing to conduct studies on this subject.
The value obtained is compared with the critical
value of the standard normal curve areas. When the
"z" value calculated is greater than the standard
normal distribution critical value, it is decided that
the mediation effect does not occur by chance, that
is, it is significant. In other words, the null hypothesis
"Ho: there is no mediating effect" is rejected and the
mediation effect is statistically significant. It is also
possible to test the significance of the mediating effect
with the confidence interval obtained for the bootstrap
distribution. Different types of confidence intervals can
be obtained based on the bootstrap method. These can
be listed as bias-corrected, percentile, bias-corrected-accelerated, etc. different types of confidence intervals.
Percentile bootstrap confidence intervals are preferred
when the variable of interest contains outliers and
the estimation is less affected by these outliers; i.e.,
robust,[12] and when the sample size is smaller than
"50".[13] When the sample size is large, the biascorrected
bootstrap method is used as an alternative to
the percentile bootstrap interval. Since the bootstrap
method corrects for bias in the sample distribution, it
provides a more reliable interval.[14] The confidence
interval obtained according to the bootstrap percentile
method is based on two percentile cut-off points for the
sample distribution (e.g., 2.5% and 97.5% for ?=0.05).
If the confidence interval for the mediating effect using
percentile values contains the value "0", the hypothesis
"Ho: there is no mediating effect" is accepted. In
other words, the effect of the mediating variable
is not statistically significant. Obtaining bootstrap
confidence intervals for the mediating variable or
testing the significance of the mediating effect is quite
easy with the help of software programs developed
today. The analysis can be easily applied with the help
of the "Process" macro plug-in developed by Andrew
F. Hayes into the open access "R Project" or "SPSS"
program. In this article, only one mediating variable is
mentioned and information about the significance of
the mediating effect is given. Currently, there are many
different types of mediation models with more than
one mediating variable, where the mediating variables
are located in parallel or sequentially with respect
to each other, with the number of mediation models
exceeding "100". All of these models can be analyzed
with the help of the programs mentioned above. To give
examples of recent studies using these models, Suissa
et al.[15] examined the role of adiposity as a mediator
in the relationship between dietary glycemic load and
lipid profiles. In another study, Konig et al.[16] evaluated
the extent to which the effect of dulaglutide on
cardiovascular risk factors could statistically explain
its effects on major cardiovascular events with the
help of mediation analysis. We believe that this article,
which includes basic information about mediation
analysis, provide a guidance for researchers who are
willing to conduct studies on this subject.
1) MacKinnon DP, Fairchild AJ, Fritz MS. Mediation analysis.
Annu Rev Psychol 2007;58:593-614. doi: 10.1146/annurev.
psych.58.110405.085542.
2) Linden A, Karlson KB. Using mediation analysis to identify
causal mechanisms in disease management interventions.
Health Serv Outcomes Res Method 2013;13:86-108. doi:10.1007/s10742-013-0106-5.
3) Imai K, Keele L, Tingley D. A general approach to causal
mediation analysis. Psychol Methods 2010;15:309-34. doi:10.1037/a0020761.
4) Imai K, Keele L, Yamamoto T. Identification, inference and
sensitivity analysis for causal mediation effects. Statistical
Science 2010;25:51-71. doi: 10.1214/10-STS321.
5) MacKinnon DP. Introduction to statistical mediation analysis.
1st ed. New York: Routledge; 2008.
6) Baron RM, Kenny DA. The moderator-mediator variable
distinction in social psychological research: Conceptual,
strategic, and statistical considerations. J Pers Soc Psychol
1986;51:1173-82. doi: 10.1037//0022-3514.51.6.1173.
7) O'Leary A, Jemmott LS, Jemmott JB. Mediation analysis
of an effective sexual risk-reduction intervention for
women: The importance of self-efficacy. Health Psychol
2008;27(2S):S180-4. doi: 10.1037/0278-6133.27.2(Suppl.)
.S180.
8) Maffoni M, Sommovigo V, Giardini A, Velutti L, Setti I.
Well-being and professional efficacy among health care
professionals: The role of resilience through the mediation
of ethical vision of patient care and the moderation of
managerial support. Eval Health Prof 2022;45:381-96. doi:10.1177/01632787211042660.
9) Ohrnberger J, Fichera E, Sutton M. The relationship between
physical and mental health: A mediation analysis. Soc Sci
Med 2017;195:42-9. doi: 10.1016/j.socscimed.2017.11.008.
10) Sobel ME. Asymptotic confidence intervals for indirect
effects in structural equation models. Sociological
Methodology 1982;13:290-312. doi: 10.2307/270723.
11) Mackinnon DP, Dwyer JH. Estimating mediated effects
in prevention studies. Eval Rev 1993;17:144-58. doi:10.1177/0193841X9301700202.
12) Creedon P S, Hayes AF. Small Sample Mediation analysis:
How Far Can We Push the Bootstrap?. Poster presented at
Ohio State University, Columbus, USA: 2015.
13) Koopman J, Howe M, Hollenbeck JR, Sin HP. Small sample
mediation testing: Misplaced confidence in bootstrapped
confidence intervals. J Appl Psychol 2015;100:194-202. doi:10.1037/a0036635.
14) Efron B. Better Bootstrap confidence intervals. J Am Stat
Assoc 1987;82:171-85. doi: 10.2307/2289144.